Flight Simulation
It is important to simulate the flight of your rocket before flying for several reasons:
- Safety It's critical to choose a motor that is powerful enough for a stable flight of your rocket.
- Legality Every flying site has limits on the altitude to which you can fly and simulation will give you an idea of how high your rocket will go.
- Recovery Simulation will tell you the optimal delay time for triggering the recovery system.
This site provides data files for use with the various flight simulators. On this page is a description of simulation in general. See the simulators page for a list of existing simulator programs. There is also a simple rocket flight simulator available on this site in the motor guide.
See also John's flight physics article for more details of these forces and the calculations employed.
In-Flight Forces
There are three main forces that affect the altitude to which a rocket will fly:
![]() Thrust is the force produced by the rocket motor and is what lifts the rocket off
the ground and keeps it moving upward.
Different motors produce thrust with different profiles
and when thrust is graphed over time, the motor's "thrust curve" is produced.
Thrust is the force produced by the rocket motor and is what lifts the rocket off
the ground and keeps it moving upward.
Different motors produce thrust with different profiles
and when thrust is graphed over time, the motor's "thrust curve" is produced.
![]() Gravity is the attractive force between the rocket and the Earth.
For our purposes, we consider this to be a constant acceleration of
9.8m/s2 on the rocket.
This is the major force that the rocket motor must overcome to lift off.
Gravity is the attractive force between the rocket and the Earth.
For our purposes, we consider this to be a constant acceleration of
9.8m/s2 on the rocket.
This is the major force that the rocket motor must overcome to lift off.
![]() Drag is the friction of the rocket moving through air and slows down the rocket.
(Note that this actually affects the rocket both while rising and falling.)
Drag is proprtional to the velocity squared, which means that it increases
very quickly with increasing speed.
Drag is the friction of the rocket moving through air and slows down the rocket.
(Note that this actually affects the rocket both while rising and falling.)
Drag is proprtional to the velocity squared, which means that it increases
very quickly with increasing speed.
Another force that affect a rocket's flight is wind. However, this is usually left out of simulations and rockets are only flown in low-wind conditions.
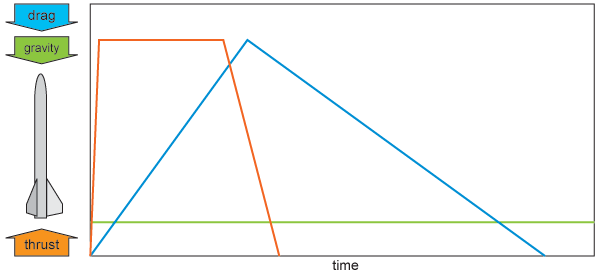
In the graph above, you can see a rough illustration of how the forces apply to a rocket in flight. Thrust simply follow's the motor's thrust curve. Gravity is a (relatively) constant force. Drag increases sharply with increasing speed (proportional the square of the velocity). Drag is highest near the end of the motor's burn (when all the thrust has been applied and maximum speed achieved).
Flight Phases
A rocket flight is broken down into several phases:
- Liftoff The moment the rocket starts its ascent.
- Powered flight The time during which the rocket is being accelerated by the motor.
- Burnout The end of the motor's burn.
- Coasting The time after motor burnout, while momentum is still causing the rocket to rise.
- Apogee The point of maximum altitude (and zero velocity), where the rocket stops rising and starts descending.
- Descent The remainder of the flight until the rocket reaches the ground.
During powered flight, the motor is providing thrust and the rocket is accelerating upward. Because of this, the velocity and drag are increasing. The thrust applied by the motor varies from moment to moment according to its characteristic burn pattern (graphed by its thrust curve). Near the end of powered fight, hobby rockets reach max Q, which is usually where "shreds" occur.
While coasting, the momentum of the rocket is still carrying it upward, but since the motor is no longer providing thrust the speed is decreasing due to gravity and drag.
The apogee point is critical in all simulations since it provides the maximum altitude reached by the rocket. The time from burnout to apogee is also important for choosing a delay time when using motor ejection since the recovery system should be triggered when the rocket is moving slowly.
Because most flight simulation is concerned with altitude achieved, the descent (or recovery) phase is usually of less interest. The simulations perfomed by the motor guide stop at apogee.
Simulation Analysis
The graphs below are from a simulation done with a simple rocket flying on an AeroTech M1939 (one of the author's favorite motors). Click on the buttons below the graph to see how the different forces and measurements change during the flight.

Thrust is the force provided by the motor. Graphing it over time produces the motor's "thrust curve." This does not include any other factors and comes from an actual static test of the motor. These files, which are specific to each motor, are the purpose of this site.
Acceleration is the sum of all forces acting on the rocket. Thrust is pushing the rocket up during the burn, gravity is pulling it down through the entire flight, and drag is slowing its speed. Note that in these graphs, negative values are chopped off at zero. This makes it appear that the acceleration reaches zero and stays there. In reality, the acceleration becomes negative when the rocket starts slowing down.
Drag is calculated from the speed of the rocket, since it is proprtional to the square of the velocity. Note how similar the drag and velocity curves are, except that the drag curve is steeper because of the square function.
Velocity is the speed the rocket is traveling. This is determined at any given point by taking the velocity at the previous point and applying the acceleration at the current point. (For rockets that stay in the lower atmosphere, max Q occurs at maximum velocity.)
Altitude is the height above ground reached by the rocket. This is determined at any given point by taking the altitude at the previous point and applying the velocity at the current point. Apogee is reached when velocity is zero, which defines the highest point reached by the rocket. Note that we stop simulating at apogee; otherwise, the altitude would drop again to zero during the descent phase.
For the mathematically minded, the acceleration is the sum of static and dynamic forces, the velocity is an integration of the acceleration, and the altitude is an integration of the velocity.
For more information on motor performance, see the motor statistics page. For a list of existing simulator programs, see the simulators page. To find motors for your rocket, try the motor guide.
